Чтобы разобраться в относительности механического движения, зададимся вопросом:

«Мы сейчас, в настоящий момент времени движемся, или находимся в состоянии покоя?»

Ты, конечно же ответишь, что всё зависит от того, что мы делаем.

Просто сидим на месте, или двигаемся куда-нибудь.

Однако это не совсем верно.

Дело в том, что даже когда ты сидишь, стоишь, или лежишь на одном и том же месте —

ты всё равно движешься!

Как это понять? Да всё очень просто. Я предполагаю, что ты сейчас находишься на планете Земля, так вот знай - она движется вокруг Солнца, и таким образом ты движешься вместе с Землёй вокруг Солнца.

Магазины и деревья на улице не стоят на месте? Стоя возле них мы же видим, что они никуда не движутся. Так движутся или нет?

Со всем разобраться поможет слово «относительно».

Давайте примем дом за неподвижное тело. Правильно оно называется тело отсчёта. Относительно его стоящие рядом деревья находятся на месте, то есть не движутся. А пролетающие рядом птицы и едущие по дороге автомобили находятся в движении.

Чтобы найти скорость движения одного тела относительно другого необходимо сложить вектора этих скоростей.

Классический закон сложения скоростей говорит:

Скорость тела относительно неподвижной системы отсчета равна геометрической сумме двух скоростей: скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной.

 

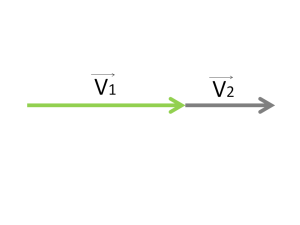
Вспомним, как складываются вектора. Пусть это будут вектора скорости V 1 и V 2

Если они направлены в одну сторону, например так:




 

Для того, чтобы их сложить нужно выстроить их друг за другом.

Это называется сложение векторов по правилу треугольника.

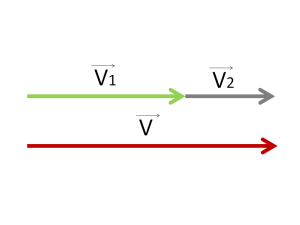
Должно получиться вот так:






 

В результате сложения таких векторов должен получиться один результирующий.

Покажем его красным цветом. Это вектор V⃗ .

Он получился, когда мы соединили начало первого вектора с концом последнего.











Два вектора V1 и V2 сложились и получился один вектор V⃗ . Всё просто.

 Бывает, что вектора могут быть направлены в разные стороны. Скажем, вот так:






 

Будем пробовать их складывать по известному правилу — правилу треугольника.

Выстроим вектора друг за другом. Должно получиться как-то так:










 

Снова соединим начало первого вектора с концом последнего.

Чтобы было лучше видно, изобразим результирующий вектор красным цветом.








 

Два вектора V⃗ 1 и V⃗ 2 сложились и получился один вектор V⃗ .

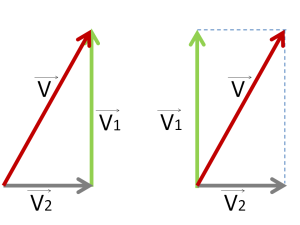
Может случиться, что вектора лежат не так ровно, а, скажем, под углом 90 градусов друг к другу.

Например:










 

Перед нами два вектора  V⃗ 1 и V⃗ 2. Как же их сложить?

Снова выстраиваем их друг за другом, чтобы получились стороны треугольника.

Или соединяем начала этих векторов — тогда получится правило параллелограмма.







 

Правило треугольника нам уже знакомо. Просто соединяем начало первого с концом последнего вектора.

Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.

Результат сложения не зависит от выбора по какому правилу складывать — треугольником или параллелограммом.

Должен получиться один и тот же вектор  V⃗ . Изобразим его красным.